Is an electron a particle or a wave? The dual nature of quantum objects

The question “Is an electron a particle or a wave?” stands at the heart of quantum physics, representing one of the most fascinating paradoxes in modern science (Feynman, 1965). This seemingly simple inquiry challenges our intuitive understanding of reality and opens the door to the bizarre and counterintuitive world of quantum mechanics. For over a century, scientists have grappled with this question, leading to revolutionary discoveries that have transformed our understanding of the physical universe from the subatomic scale to the cosmic (Crease, 2002).

When we observe everyday objects around us, we can easily categorize them as either particles (like grains of sand) or waves (like ripples on a pond). These categories seem mutually exclusive in our classical world. However, quantum physics reveals that at the microscopic level, nature isn’t so easily classified. Electrons and other quantum entities exhibit behaviors characteristic of both particles and waves, depending on how we observe them. This dual nature doesn’t merely represent our limited understanding; it appears to be a fundamental property of reality at the quantum scale.

The classical view: Particles vs. waves

Before diving into quantum mechanics, it’s helpful to understand the classical distinction between particles and waves, as this forms the foundation for appreciating the revolutionary nature of quantum physics.

Classical particles

In classical physics, particles are discrete objects with definite positions in space. They have distinct boundaries and properties like mass, charge, and momentum. A particle follows a well-defined trajectory through space, much like a baseball thrown across a field or a billiard ball rolling across a table. Particles interact through direct contact or through fields, and their motion can be precisely calculated using Newton’s laws of motion.

Key characteristics of classical particles include:

• Localized in space with definite position and momentum
• Discrete and indivisible entities
• Interact through contact or fields
• Follow deterministic trajectories

Classical waves

In contrast, classical waves are disturbances that propagate through space or a medium. Unlike particles, waves are extended entities that don’t exist at a single point but spread out across regions of space. Ocean waves, sound waves, and light waves (in classical electromagnetics) are all examples of wave phenomena. Waves can interfere with one another, creating patterns of constructive and destructive interference, and they can diffract around obstacles.

Key characteristics of classical waves include:

• Extended in space rather than localized
• Can interfere with one another
• Can diffract around obstacles
• Carry energy without transporting matter

For centuries, scientists maintained a clear distinction between particles and waves. Matter was composed of particles, while phenomena like light and sound were explained as waves. This neat categorization worked remarkably well for explaining most everyday experiences and formed the basis of classical physics.

However, as scientists developed more sophisticated experiments and peered deeper into the microscopic world, this clean distinction began to blur. The first hints of trouble came from studies of light, which exhibited both wave-like and particle-like properties. Eventually, this wave-particle confusion would extend to matter itself, most notably with electrons, leading to one of the most profound scientific revolutions in history.

The electron as a particle: Historical perspective

The journey to understanding electrons began firmly in the particle camp. The discovery and early characterization of electrons established them as fundamental particles of matter with specific properties that seemed to confirm their particle nature.

Discovery of the electron

The electron was discovered in 1897 by British physicist J.J. Thomson through his experiments with cathode ray tubes (Thomson, 1897). These vacuum tubes contained two electrodes that, when charged with high voltage, produced a beam of what Thomson called “corpuscles” (later renamed electrons) that traveled from the negative electrode (cathode) to the positive electrode (anode).

Thomson observed that these beams could be deflected by both electric and magnetic fields, indicating they carried a negative electric charge. By measuring the degree of deflection, he calculated the charge-to-mass ratio of these particles, demonstrating that they were much lighter than hydrogen atoms (the lightest known particles at the time). Thomson’s work led to the crucial understanding that electrons were fundamental, subatomic particles carrying a negative charge.

The Millikan oil drop experiment

Robert Millikan’s famous oil drop experiment in 1909 further confirmed the particle nature of electrons by precisely measuring their charge. Millikan sprayed tiny oil droplets into a chamber with charged plates above and below. By adjusting the voltage between the plates and observing the movement of the droplets, he was able to calculate the charge of a single electron.

This experiment was revolutionary because it showed that electric charge came in discrete units, confirming the particulate nature of electrons. Millikan determined the charge of an electron to be approximately 1.6 × 10^-19 coulombs, remarkably close to the currently accepted value.

Electron properties consistent with particles

Several properties of electrons seemed to confirm their status as particles:

1. Mass: Electrons have a specific, constant rest mass of approximately 9.11 × 10^-31 kilograms.
2. Charge: Electrons carry a fixed negative charge of -1.602 × 10^-19 coulombs.
3. Point-like nature: Electrons appeared to be point-like particles in many experiments, with no measurable physical size.
4. Deflection in fields: Electrons follow curved paths in electric and magnetic fields, consistent with charged particles.
5. Discrete impacts: Electrons create distinct points of impact when they strike photographic plates or phosphorescent screens.

These observations reinforced the view of electrons as discrete particles, fitting neatly into the classical particle model. For many early applications, including the development of vacuum tubes and early electronics, this particle model of electrons was entirely adequate.

However, as scientists conducted more sophisticated experiments in the early 20th century, unexpected behaviors began to emerge that couldn’t be explained by treating electrons solely as particles. These puzzling observations would eventually lead to a radical rethinking of the electron’s nature.

The electron as a wave: Challenging the particle paradigm

While early experiments supported the particle nature of electrons, a series of groundbreaking discoveries in the early 20th century began to suggest that electrons could also behave like waves. This revolutionary idea challenged the fundamental assumptions of classical physics and opened the door to the quantum realm.

Louis de Broglie’s matter waves

In 1924, French physicist Louis de Broglie made an audacious proposal in his doctoral thesis (de Broglie, 1924). Inspired by Einstein’s work showing that light could behave as both waves and particles, de Broglie suggested that all matter, including electrons, should exhibit wave-like properties. He proposed that any moving particle has an associated wavelength (λ) related to its momentum (p) by the equation:

λ = h/p

where h is Planck’s constant (approximately 6.63 × 10^-34 joule-seconds).

According to this equation, the wavelength of macroscopic objects would be incredibly small and undetectable, explaining why we don’t observe wave-like behavior in everyday objects. However, for tiny particles like electrons, the wavelength could be significant enough to produce observable wave effects.

De Broglie’s hypothesis was initially met with skepticism. After all, how could a discrete particle like an electron also behave as a spread-out wave? His idea seemed almost metaphysical. However, it wouldn’t be long before experimental evidence provided stunning confirmation of de Broglie’s matter waves.

The Davisson-Germer experiment

The definitive experimental proof of electron waves came in 1927 through the work of Clinton Davisson and Lester Germer at Bell Labs (Davisson & Germer, 1927). Initially, they weren’t trying to test de Broglie’s hypothesis—they were studying the surface properties of nickel by bombarding it with electrons. However, after accidentally oxidizing their nickel sample and then recrystallizing it through heating, they observed something unexpected.

When they directed a beam of electrons at their nickel crystal, the reflected electrons formed an interference pattern. This pattern was remarkably similar to the diffraction patterns produced when X-rays (known to be waves) were scattered by crystals. The electron beam was behaving exactly as a wave would, with the electrons diffracting off the regular lattice of atoms in the crystal.

The Davisson-Germer experiment provided compelling evidence that electrons could indeed behave like waves. The wavelength of the electron waves calculated from their diffraction pattern matched precisely with de Broglie’s formula, confirming his revolutionary hypothesis.

Electron diffraction and interference

Following the Davisson-Germer experiment, other researchers quickly performed additional experiments that further confirmed the wave nature of electrons:

1. G.P. Thomson experiment: In 1927, G.P. Thomson (ironically, the son of J.J. Thomson who had discovered the electron as a particle) passed a beam of electrons through a thin metal foil and observed circular diffraction patterns on a photographic plate behind it (Thomson, 1927). These patterns were identical to those produced by X-rays, providing further evidence of the wave nature of electrons.
2. Electron microscopy: The wave properties of electrons became the foundation for electron microscopy, a technique that uses electron beams instead of light to create images. Because electrons can have much shorter wavelengths than visible light, electron microscopes can achieve much higher resolution than optical microscopes.
3. Single-electron interference: Perhaps most remarkably, when electrons are sent one by one through a double-slit apparatus (similar to Thomas Young’s famous double-slit experiment with light), they gradually build up an interference pattern on a detector screen. This demonstrates that even individual electrons exhibit wave-like behavior, interfering with themselves as they pass through both slits simultaneously.

These experiments conclusively demonstrated that electrons possess wave-like properties, forcing scientists to reconsider the fundamental nature of matter and energy. The electron could no longer be classified as simply a particle or a wave—it seemed to be both, or perhaps something entirely different that manifested these dual aspects depending on how it was observed.

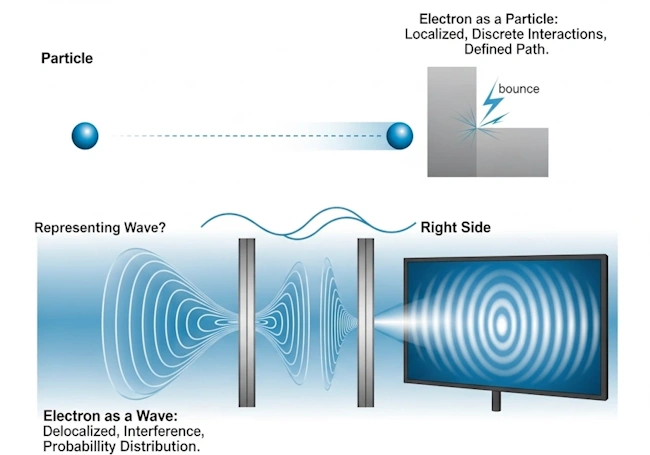
The double-slit experiment: Witnessing the paradox

The double-slit experiment stands as perhaps the most iconic demonstration of the wave-particle duality of electrons and other quantum entities (Crease, 2002). Originally performed with light by Thomas Young in 1801 to demonstrate the wave nature of light, this experiment was later adapted for electrons with astonishing results that revealed the heart of quantum weirdness (Jönsson, 1961).

Setup and classical expectations

The basic setup of the double-slit experiment is deceptively simple:

1. A source emits electrons (or other particles/waves)
2. The electrons pass through a barrier with two narrow, parallel slits
3. The electrons are detected on a screen behind the barrier

If electrons were purely classical particles, we would expect them to pass through either one slit or the other, creating two distinct bands on the detection screen directly behind each slit. Just like firing bullets through two holes would create two distinct clusters of impacts.

If electrons were purely classical waves, we would expect them to pass through both slits simultaneously, creating an interference pattern on the detection screen. This pattern would consist of alternating bright and dark bands (called fringes) resulting from constructive and destructive interference of the waves.

What actually happens

When scientists performed this experiment with electrons, the results were mind-boggling:

1. With both slits open: Electrons created an interference pattern on the detector screen, with alternating bands of high and low electron detection probability. This strongly suggested that electrons were behaving as waves, diffracting through both slits and interfering with themselves.
2. Electron by electron: Even more remarkably, when electrons were sent through the apparatus one at a time (ensuring no possibility of interaction between electrons), the same interference pattern gradually emerged over time. Each individual electron seemed to “know” about the overall interference pattern that would eventually form.
3. Detection at the slits: When scientists attempted to determine which slit each electron passed through by placing detectors at the slits, something extraordinary happened. The mere act of observing the electrons caused the interference pattern to disappear, replaced by the two-band pattern expected for classical particles. The electrons essentially “collapsed” into particle-like behavior when observed.

The measurement problem

This last observation highlights what physicists call the “measurement problem” in quantum mechanics. The act of measurement or observation seems to fundamentally alter the behavior of quantum systems. When left unobserved, electrons behave like waves, capable of taking multiple paths simultaneously and interfering with themselves. When observed, they behave like particles following a single, definite path.

This isn’t just a limitation of our measurement techniques—it appears to be a fundamental aspect of quantum reality. The electron doesn’t have definite particle or wave properties independent of observation; rather, the act of measurement itself seems to determine which aspect of its dual nature becomes manifest.

The double-slit experiment with electrons doesn’t just demonstrate that electrons have both particle and wave aspects—it suggests that these aspects are complementary. We can’t observe both simultaneously, and the type of experiment we choose determines which aspect we’ll observe. This complementarity is a central feature of quantum mechanics and highlights why the question “Is an electron a particle or a wave?” is ultimately misleading. The answer isn’t one or the other, but both and neither at the same time.

Quantum mechanics: A framework for duality

To accommodate the strange dual nature of electrons and other quantum entities, physicists needed to develop an entirely new theoretical framework. This framework, quantum mechanics, represents one of the most successful scientific theories ever developed, capable of explaining the behavior of matter and energy at the smallest scales with unprecedented accuracy.

The Schrödinger equation and wave functions

At the heart of quantum mechanics is the Schrödinger equation, developed by Austrian physicist Erwin Schrödinger in 1925 (Schrödinger, 1926). This equation describes how quantum systems evolve over time and introduces the concept of the wave function (typically denoted by the Greek letter ψ, pronounced “psi”).

The wave function is a mathematical function that contains all the information about a quantum system, such as an electron. It represents not the physical electron itself, but rather the probability of finding the electron in various locations. The square of the wave function (|ψ|²) at any point gives the probability density of finding the particle at that location when measured.

Unlike classical particles that have definite positions at all times, the wave function of an electron can be spread out across space, reflecting the wave-like nature of the electron. When we make a measurement to determine the electron’s position, the wave function is said to “collapse,” and we observe the electron at a specific location.

Heisenberg’s uncertainty principle

Another cornerstone of quantum mechanics is Heisenberg’s uncertainty principle, formulated by Werner Heisenberg in 1927 (Heisenberg, 1927). This principle states that there is a fundamental limit to the precision with which complementary properties of a quantum system, such as position and momentum, can be simultaneously known.

Mathematically, the uncertainty principle is expressed as:

Δx × Δp ≥ ħ/2

where Δx is the uncertainty in position, Δp is the uncertainty in momentum, and ħ is the reduced Planck constant (h/2π).

This principle isn’t just a limitation of our measuring instruments but a fundamental property of quantum systems. It’s intimately related to the wave-particle duality: a wave is spread out in space (well-defined wavelength/momentum) but not localized (poorly defined position), while a particle is localized (well-defined position) but not spread out (poorly defined wavelength/momentum).

Wave-particle duality as complementarity

Danish physicist Niels Bohr introduced the concept of complementarity to make sense of wave-particle duality (Bohr, 1928). According to Bohr, wave and particle aspects of quantum entities are complementary properties that cannot be observed simultaneously. The type of measurement we perform determines which aspect becomes manifest.

Complementarity suggests that asking whether an electron is “really” a particle or “really” a wave is a misguided question. Both descriptions are necessary for a complete understanding, but they apply in different experimental contexts. The electron isn’t simply a particle with wave properties or a wave with particle properties—it’s a quantum entity that transcends classical categorization.

Quantum field theory perspective

In modern physics, quantum field theory (QFT) provides an even deeper perspective on the nature of electrons. In QFT, particles like electrons are viewed as excited states of underlying quantum fields that permeate all of space. This framework unifies the particle and wave aspects by treating both as manifestations of the same underlying quantum field.

From this perspective, what we call an “electron” is an excitation of the electron field, much like a water wave is an excitation of the water’s surface. When we observe particle-like behavior, we’re detecting localized excitations of the field. When we observe wave-like behavior, we’re detecting the field’s extended wave-like properties.

Quantum mechanics thus provides a consistent mathematical framework that accommodates both the particle and wave aspects of electrons, resolving the apparent paradox through a profound revision of our understanding of physical reality at the quantum scale.

Real-world implications of electron duality

The wave-particle duality of electrons isn’t just a fascinating theoretical concept—it has profound practical implications that have transformed modern technology and our understanding of the physical world. From the development of sophisticated microscopes to the design of modern electronic devices, the dual nature of electrons has both practical applications and philosophical implications.

Electron microscopy

One of the most direct applications of electron wave properties is electron microscopy. Conventional optical microscopes are limited by the wavelength of visible light, which restricts their resolution to about 200 nanometers. However, according to de Broglie’s relationship, electrons accelerated to high energies have wavelengths much shorter than visible light.

Transmission electron microscopes (TEMs) and scanning electron microscopes (SEMs) exploit this property to achieve resolutions down to the atomic scale. By using electrons rather than photons, these microscopes can reveal structures thousands of times smaller than what can be seen with optical microscopes. This capability has revolutionized fields ranging from materials science to biology, allowing scientists to directly visualize viruses, molecular structures, and the atomic lattices of crystals.

Quantum tunneling and electronic devices

Another quantum phenomenon that arises from electron wave properties is quantum tunneling. According to classical physics, a particle cannot pass through a barrier if it doesn’t have enough energy to overcome it. However, the wave function of an electron can extend beyond such barriers, giving the electron a small but non-zero probability of appearing on the other side—effectively “tunneling” through the barrier.

This seemingly esoteric effect is actually crucial for many modern electronic devices:

1. Tunnel diodes: These specialized diodes use quantum tunneling to achieve extremely fast switching speeds, useful in high-frequency applications.
2. Flash memory: The memory cells in flash drives and solid-state drives work by storing electrons that have tunneled through an insulating barrier.
3. Scanning tunneling microscopy (STM): This technique uses the tunneling of electrons between a sharp probe tip and a surface to image individual atoms on surfaces.
4. Quantum computing: Many quantum computing architectures rely on tunneling effects for their operation.

Semiconductor physics

The entire field of semiconductor physics, which underlies all modern computing devices, depends on understanding both the particle and wave aspects of electrons. Semiconductor devices work by controlling the movement of electrons through materials like silicon, and their design requires accounting for both the discrete particle-like behavior of electrons and their wave-like properties.

For example, in a transistor (the fundamental building block of digital electronics), electrons behave as particles when they flow as current through a channel, but their distribution within the semiconductor follows patterns predicted by quantum wave functions. The miniaturization of electronic components has pushed device dimensions so small that quantum effects, including wave interference and tunneling, become increasingly important in device operation.

Quantum chemistry and materials science

The wave nature of electrons is essential for understanding chemical bonding and the electronic properties of materials. In quantum chemistry, electrons aren’t visualized as tiny particles orbiting the nucleus like planets around the sun (the Bohr model) but as probability clouds described by wave functions (the quantum mechanical model).

This quantum mechanical understanding of electron behavior has enabled:

1. The development of new materials with tailored electronic properties
2. Accurate prediction of chemical reactions and molecular structures
3. Design of catalysts for industrial processes
4. Advancement of technologies like solar cells and battery materials

The dual nature of electrons has thus been instrumental in the technological revolution of the past century, enabling tools and technologies that would be impossible under a purely classical understanding of physics.

Philosophical implications: What does it all mean?

The wave-particle duality of electrons doesn’t just challenge our technical understanding of physics—it raises profound philosophical questions about the nature of reality, measurement, and our ability to comprehend the quantum world. These questions have engaged physicists and philosophers alike for nearly a century, leading to various interpretations of quantum mechanics.

The Copenhagen interpretation

The traditional view, known as the Copenhagen interpretation and developed primarily by Niels Bohr and Werner Heisenberg, suggests that quantum systems exist in a superposition of all possible states until measured (Wheeler & Zurek, 1983). Measurement causes the “collapse” of the wave function into a definite state.

Under this interpretation, properties like “position” or “momentum” don’t have definite values until they are measured. The act of observation doesn’t just reveal pre-existing properties but actually plays a role in determining them. This view challenges our intuitive notion that physical objects have well-defined properties independent of observation.

Critics of the Copenhagen interpretation, including Einstein, found this view problematic. Einstein famously objected to the probabilistic nature of quantum mechanics, remarking that “God does not play dice with the universe.” He believed that quantum mechanics, while practically useful, must be incomplete, with “hidden variables” that would restore determinism and realism to physics (Bohm, 1952).

Many-worlds interpretation

An alternative view, proposed by Hugh Everett III in 1957, is the many-worlds interpretation (Wheeler & Zurek, 1983). This interpretation suggests that every possible outcome of a quantum measurement occurs, but in different “branches” of the universe that cannot interact with each other. In this view, when we measure an electron’s position, the universe splits into multiple branches—one for each possible position where the electron could be found.

This interpretation preserves mathematical determinism at the cost of an enormous proliferation of parallel universes. It eliminates the special role of measurement but introduces the metaphysical challenge of accepting countless parallel realities.

Quantum decoherence

More recent approaches focus on quantum decoherence—the process by which quantum systems interact with their environment, causing quantum superpositions to rapidly become undetectable (Zurek, 2003). Decoherence explains why quantum effects like superposition are readily observable for isolated systems like individual electrons but seemingly absent in macroscopic objects (Arndt & Hornberger, 2014).

Under this view, the apparent “collapse” of the wave function isn’t a fundamental process but rather the result of entanglement between the quantum system and its environment. This perspective helps bridge the gap between the quantum and classical worlds, explaining why our everyday experience appears classical despite the quantum nature of its constituents.

The measurement problem revisited

The philosophical tension at the heart of quantum mechanics—often called the measurement problem—remains unresolved. What exactly constitutes a “measurement”? How do we reconcile the probabilistic nature of quantum systems with the apparent determinism of the macroscopic world?

These questions continue to inspire research in foundations of quantum mechanics (Zeilinger, 1999). Recent experimental advances have made it possible to create and maintain quantum superpositions in increasingly large systems, pushing the boundary between the quantum and classical worlds and shedding new light on these fundamental questions (Arndt & Hornberger, 2014).

What’s particularly fascinating is that despite these philosophical uncertainties, quantum mechanics works extraordinarily well as a practical theory. Engineers can design semiconductor devices, scientists can develop new materials, and researchers can manipulate individual quantum systems—all using a theory whose philosophical foundations remain contested.

References:

1. Arndt, M., & Hornberger, K. (2014). Testing the limits of quantum mechanical superpositions. Nature Physics, 10(4), 271-277.
2. Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Physical Review, 85(2), 166-179.
3. Bohr, N. (1928). The quantum postulate and the recent development of atomic theory. Nature, 121(3050), 580-590.
4. Davisson, C., & Germer, L. H. (1927). Diffraction of electrons by a crystal of nickel. Physical Review, 30(6), 705-740.
5. de Broglie, L. (1924). Recherches sur la théorie des quanta (Researches on the quantum theory). Thesis, Paris.
6. Feynman, R. P. (1965). The Feynman Lectures on Physics, Vol. III: Quantum Mechanics. Addison-Wesley.
7. Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43(3-4), 172-198.
8. Jönsson, C. (1961). Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Zeitschrift für Physik, 161(4), 454-474.
9. Schrödinger, E. (1926). Physical Review, 28(6), 1049-1070.
10. Thomson, G. P. (1927). Experiments on the diffraction of cathode rays. Proceedings of the Royal Society of London. Series A, 117(778), 600-609.
11. Thomson, J. J. (1897). Cathode rays. Philosophical Magazine, 44(269), 293-316.
12. Wheeler, J. A., & Zurek, W. H. (Eds.). (1983). Quantum Theory and Measurement. Princeton University Press.
13. Zurek, W. H. (2003). Reviews of Modern Physics, 75(3), 715-775.
14. Zeilinger, A. (1999). Experiment and the foundations of quantum physics. Reviews of Modern Physics, 71(2), S288-S297.
15. Crease, R. P. (2002). The most beautiful experiment. Physics World, 15(9), 19-20.