What is quantum tunneling?

Introduction: a gateway between worlds

In classical physics, a ball rolling toward a hill will either surmount it if it possesses sufficient energy, or it will roll backward if it lacks that energy. This intuitive understanding has governed our perception of the physical world for centuries.

Yet at the quantum scale, nature operates according to fundamentally different rules. Electrons, protons, and other subatomic particles exhibit a remarkable ability to traverse barriers that classical physics forbids them from crossing—a phenomenon known as quantum tunneling. This counterintuitive process, where particles appear on the opposite side of a potential energy barrier despite lacking the energy to overcome it classically, stands as one of the most profound and consequential discoveries in physics.

Far from being a mere theoretical curiosity, quantum tunneling forms the foundation of technologies ranging from flash memory to quantum computers and illuminates the mechanisms powering stellar fusion in the hearts of distant stars.

The classical paradox: why quantum tunneling challenges our understanding

To fully appreciate quantum tunneling, we must first confront the limitations of classical mechanics when applied to the microscopic realm.

In classical physics, the energy of a particle determines its trajectory. A particle with total energy E encounters a potential energy barrier of height V₀. If E < V₀, classical mechanics predicts with absolute certainty that the particle cannot penetrate the barrier—it is entirely forbidden from entering the region where potential energy exceeds its total energy.

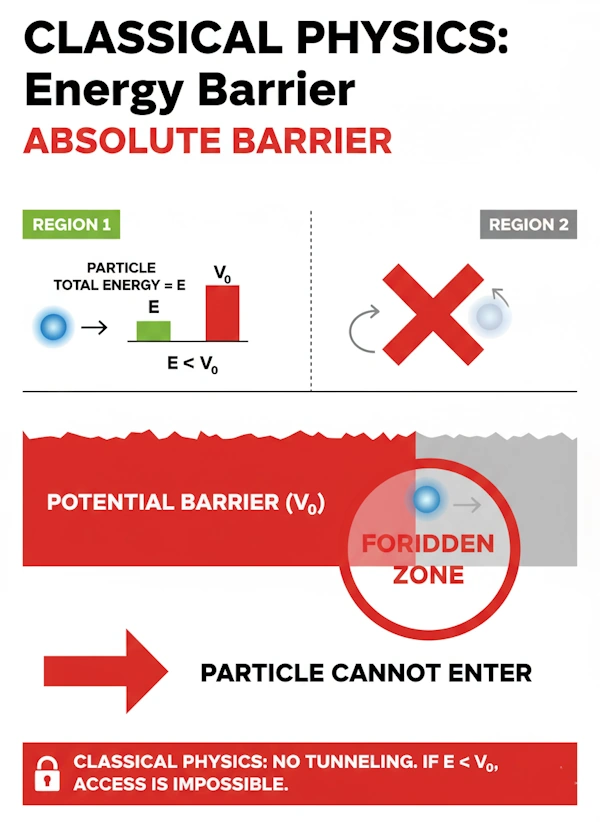
However, this picture breaks down at atomic and subatomic scales. In the early 20th century, as physicists constructed their new theory of quantum mechanics to explain phenomena classical physics could not address, a puzzling observation came to light: particles were regularly found on the opposite side of barriers they should never have been able to cross. Alpha particles escaped from atomic nuclei.

Electrons tunneled through insulating layers. The universe, it seemed, had not received the memo about classical forbidden regions.

This discrepancy between observation and classical prediction was not a flaw in experimental apparatus or measurement technique. Rather, it revealed a fundamental truth about nature that demanded an entirely new theoretical framework to explain.

Wave-particle duality

The resolution to this paradox lies in one of quantum mechanics’ most revolutionary insights: matter possesses both particle and wave characteristics. In 1923, Louis de Broglie proposed that particles exhibit wave-like properties, with a wavelength inversely proportional to their momentum. This insight transformed how physicists conceptualized subatomic phenomena.

The Schrödinger equation, published in 1926 by Erwin Schrödinger, provided the mathematical framework for this wave-particle duality. Rather than describing a particle’s position with certainty, the Schrödinger equation describes the quantum state of a system through a wave function—a mathematical function that contains all knowable information about the system.

Crucially, the wave function does not abruptly terminate at the boundaries of a potential barrier. Instead, it exhibits wave-like behavior, decaying exponentially into and through the barrier.

The absolute value squared of the wave function yields the probability distribution for finding the particle at a given location. Even within a classically forbidden region—where the particle should have zero probability of existing—the wave function remains nonzero, albeit exponentially small.

This is the fundamental insight that permits quantum tunneling: if the wave function extends through a barrier, there exists a finite probability that a measurement will find the particle on the opposite side, having tunneled through what classical physics considered an impenetrable wall.

Mathematical description: the WKB approximation

While exact solutions to the Schrödinger equation exist only for idealized barrier geometries, physicists developed the WKB approximation (named after Wentzel, Kramers, and Brillouin) to calculate tunneling probabilities for realistic potentials. This semiclassical method treats the wave function as an exponential function that varies slowly across distances comparable to the de Broglie wavelength.

For a particle of mass m and energy E encountering a one-dimensional potential barrier, the transmission coefficient—the probability that the particle tunnels through—is given by an exponential decay factor. The transmission probability depends critically on three factors: the barrier height (V₀ – E), the barrier width (a), and the particle’s mass (m). The mathematical relationship reveals why tunneling is exponentially sensitive to these parameters.

Importantly, the transmission coefficient decreases exponentially with both increasing barrier width and increasing barrier height. This extreme sensitivity to barrier dimensions explains why tunneling is a dominant phenomenon for electrons passing through barriers just a few nanometers thick, but becomes vanishingly small for macroscopic objects. It also explains why lighter particles, such as electrons and protons, tunnel far more readily than heavier particles.

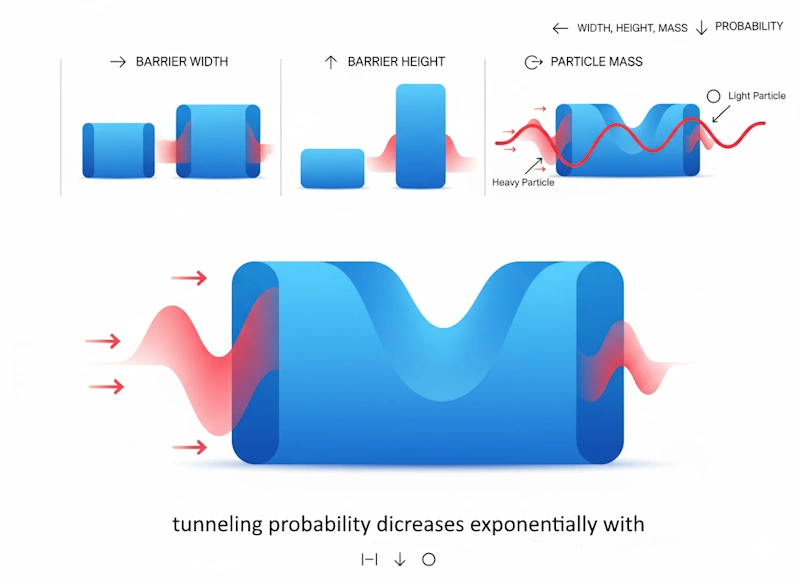
The WKB approximation assumes that the potential varies slowly compared to the particle’s de Broglie wavelength. While not exact, it provides remarkably accurate predictions for tunneling rates and decay constants, making it an indispensable tool in quantum physics applications.

Historical development: from theory to verification

The journey from theoretical prediction to experimental confirmation shaped the course of 20th-century physics. In 1927, Friedrich Hund became the first to apply the Schrödinger equation to tunneling problems, studying double-well potentials in molecular systems. That same year, Leonid Mandelstam and Mikhail Leontovich independently discovered the tunneling effect. However, the most dramatic early application emerged in nuclear physics.

In 1928, George Gamow provided a theoretical explanation for alpha decay—the radioactive emission of alpha particles from unstable nuclei—using quantum tunneling.

Independently, Ronald Gurney and Edward Condon developed the same explanation. This was profoundly significant: the half-lives of alpha-emitting elements vary over 20 orders of magnitude, from microseconds to billions of years, while the energy of emitted alpha particles varies by only a factor of two. This enormous range in decay rates, dependent sensitively on energy, could only be explained by an exponential process—exactly what quantum tunneling predicts. The extraordinary success of tunneling theory in explaining radioactive decay provided early experimental confirmation that quantum mechanics accurately described nature at the nuclear scale.

The terminology itself evolved during this era. The German physicist Walter Schottky used the term “wellenmechanischer Tunneleffekt” (wave-mechanical tunnel effect) in 1931.

By 1932, when Yakov Frenkel introduced the English term “tunnel effect” in his textbook, the concept had become firmly established in physics.

The 1950s and 1960s brought revolutionary technological applications. In 1957, Leo Esaki demonstrated electron tunneling through thin barriers in semiconductor structures and developed the tunnel diode.

In 1960, Ivar Giaever extended this work to superconductors, providing direct evidence of the superconducting energy gap through tunneling spectroscopy.

In 1962, Brian Josephson predicted superconducting tunneling of Cooper pairs, leading to the discovery of the Josephson effect.

Their collective contributions earned Esaki, Giaever, and Josephson the 1973 Nobel Prize in Physics.

Perhaps most dramatically, in 1981-1982, Gerd Binnig and Heinrich Rohrer developed the scanning tunneling microscope (STM) by exploiting electron tunneling through a nanometer-scale vacuum gap. Their invention, recognized with the 1986 Nobel Prize in Physics, revolutionized materials science by enabling direct atomic-scale imaging and manipulation of surfaces.

Most recently, in 2025, John Clarke, Michel Devoret, and John Martinis received the Nobel Prize for demonstrating macroscopic quantum tunneling in electrical circuits—showing that billions of particles acting collectively could exhibit tunneling behavior, fundamentally expanding the scope of the phenomenon.

Real-world applications: where quantum tunneling shapes technology

Nuclear fusion and stellar processes

The stars furnish perhaps the most profound application of quantum tunneling. In the core of our Sun and other stars, temperatures reach millions of degrees, yet remain insufficient by classical calculations for hydrogen nuclei to overcome their mutual Coulomb repulsion and fuse. Classical physics predicts that stellar fusion should be impossible, and our Sun should not burn.

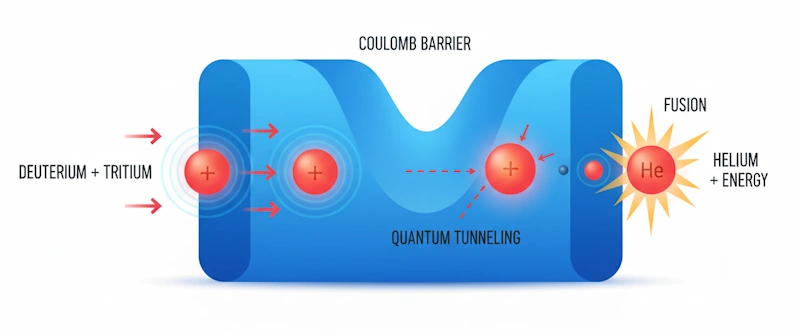
Quantum tunneling resolves this apparent contradiction. The thermal motion of protons gives them not just one opportunity to fuse, but countless collisions. Even though each individual nucleus lacks sufficient energy to classically surmount the Coulomb barrier, quantum tunneling provides a finite probability for fusion at each encounter.

The exponential sensitivity of the tunneling probability to energy variations means that modest temperature increases dramatically enhance fusion rates. While each individual fusion event remains probabilistically unlikely, the enormous number of nuclei in a stellar core ensures that fusion proceeds at the observed rate, sustaining stellar nucleosynthesis and releasing the energy that lights the cosmos.

Without quantum tunneling, stars would be cold, dark objects, and life as we know it could not exist.

Similarly, tunneling enables nucleosynthesis of heavy elements in supernovae and neutron star mergers, processes central to understanding how the elements we depend on for life were forged in stellar furnaces.

Radioactive decay and nuclear physics

The nuclear domain of terrestrial physics depends fundamentally on quantum tunneling. Alpha decay—the emission of alpha particles (helium-4 nuclei) from heavy unstable atoms—demonstrates this dependence dramatically.

Consider uranium-238, which emits an alpha particle with approximately 4.3 MeV of kinetic energy, yet experiences a nuclear binding energy barrier (including Coulomb repulsion) exceeding 6 MeV. Classically, the alpha particle should remain permanently trapped. Yet it escapes with a half-life of 4.5 billion years—a timescale that enables radiometric dating of ancient rocks and meteorites.

The stark dependence of decay rates on alpha particle energy exemplifies tunneling’s exponential sensitivity. Uranium-235 emits alpha particles with slightly lower energy (4.4 MeV instead of 4.3 MeV) yet has a half-life 14 times longer.

This enormous change from a modest energy variation reflects the exponential dependence predicted by WKB theory.

The same phenomenon enables medical applications (radioisotope production for diagnostics and therapy) and finds application in nuclear forensics and archaeology.

Semiconductor devices and electronics

The modern electronic era was launched by engineering applications of quantum tunneling. The tunnel diode, developed following Esaki’s groundbreaking work, exploits the extreme dependence of tunneling current on barrier thickness to achieve switching speeds and performance characteristics impossible with conventional diodes.

Flash memory—the technology powering USB drives, solid-state drives (SSDs), and smartphones—depends on quantum tunneling for both data storage and erasure. In flash memory cells, electrons tunnel through a thin silicon dioxide insulating layer to enter and exit a floating gate electrode. By controlling the number of trapped electrons, the memory cell stores charge that represents digital information. Reading the stored charge and erasing it via reverse tunneling enables the rewritable storage that has revolutionized portable computing.

As transistor dimensions shrink below 1 nanometer—a trend governed by Moore’s Law—tunneling current leakage through insulating layers becomes increasingly problematic. Electrons tunnel readily through oxides just nanometers thick, creating unwanted current leakage that wastes power, generates heat, and limits device performance.

Understanding and controlling this tunneling represents one of microelectronics’ central challenges as the industry pushes transistors toward their physical limits.

Scanning tunneling microscopy: imaging at the atomic scale

The scanning tunneling microscope stands as perhaps the most elegant practical application of quantum tunneling. The STM allows direct visualization of individual atoms on conductive surfaces—a capability that seemed impossible when developed, since atoms are far smaller than visible light wavelengths.

The STM operates by positioning an extremely sharp metallic tip (ideally terminating in a single atom) approximately 0.1-1 nanometer from a conductive sample surface. A small voltage (0.1-3 volts) applied between tip and sample creates an electric field that permits electrons to tunnel across the nanometer-scale vacuum gap. As the tip rasters across the sample surface, the tunneling current varies exponentially with tip-sample separation. A feedback loop maintains constant tunneling current by adjusting the tip height, thereby mapping the surface topography with atomic-scale precision. Lateral resolution reaches 0.1 nanometers while vertical resolution surpasses 0.01 nanometers.

The STM’s revolutionary capability came from recognizing that the extreme sensitivity of tunneling current to distance—decreasing exponentially with separation—could be exploited as a spectacularly sensitive distance sensor. No other microscopy technique achieves comparable resolution without damaging the sample, and no other technique permits direct manipulation of individual atoms and molecules on surfaces.

STM applications range from studying fundamental surface physics and characterizing semiconductor structures to investigating biological molecules and engineering nanostructures atom-by-atom. The technique has revealed atomic-scale details of molecular assemblies, corrosion processes, catalytic reactions, and countless other phenomena, revolutionizing materials science and nanotechnology.

Quantum computing

The most recent and potentially most transformative application of quantum tunneling appears in quantum computing. The 2025 Nobel Prize in Physics recognized discoveries in macroscopic quantum tunneling that directly led to superconducting qubits—the artificial atoms used in modern quantum computers.

Superconducting qubits are engineered quantum systems consisting of superconducting circuits incorporating Josephson junctions. A Josephson junction comprises two superconductors separated by a thin insulating barrier. Quantum tunneling permits Cooper pairs—paired electrons in the superconducting state—to tunnel across the junction. The tunneling probability can be controlled via external magnetic and electrical fields, enabling precise manipulation of quantum states.

By designing circuits with carefully chosen capacitances and inductances, engineers create artificial atoms exhibiting two distinct energy levels, analogous to atomic electrons. These serve as quantum bits (qubits). The non-linearity provided by the Josephson junction’s tunneling effect ensures that the two-qubit states remain isolated from higher energy levels—essential for qubit fidelity.

Current quantum computers from IBM, Google, and other companies employ superconducting qubits as their fundamental processing units. Google’s 2019 quantum supremacy experiment used a 53-qubit superconducting processor, while IBM has demonstrated systems with 127 qubits. These machines exploit quantum tunneling to enable quantum superposition and entanglement—properties permitting quantum computers to explore vast computational spaces far more efficiently than classical computers for specific problem classes.

Mechanisms and physical interpretation

The wave function and probability

Quantum tunneling fundamentally reflects the probabilistic interpretation of quantum mechanics. The wave function itself does not directly represent physical reality in any simple way. Rather, it provides a complete description of the quantum system, from which all measurable quantities can be extracted. The wave function’s absolute value squared yields the probability density—the likelihood of finding the particle at a given location upon measurement.

For a particle encountering a rectangular potential barrier of height V₀, width a, and total energy E < V₀, the wave function oscillates in classically allowed regions but decays exponentially within the barrier. In standard interpretation, the penetration of the wave function into the forbidden region represents nonzero probability for finding the particle there. Upon measurement, the wave function “collapses” to reveal the particle’s location. If measured beyond the barrier, the particle is found to have tunneled through.

The transmission coefficient and tunneling probability

For realistic potential shapes, the WKB approximation yields a transmission coefficient T that depends exponentially on the tunneling exponent γ. For a particle of mass m tunneling through a barrier from classical turning point x₁ to x₂:

γ = (1/ℏ) ∫[x₁ to x₂] √[2m(V(x) – E)] dx

The transmission coefficient is approximately T ≈ e^(-2γ), revealing the exponential dependence on barrier properties. This formula encapsulates why tunneling becomes exponentially more probable for lighter particles, narrower barriers, and higher particle energies approaching the barrier height.

Distance dependence

An especially remarkable feature of tunneling is its extreme sensitivity to distance. The tunneling current in the STM decreases exponentially with tip-sample separation, typically decreasing by a factor of 10 for every 0.1 nanometer increase in distance. This extraordinary sensitivity enabled the STM’s unprecedented resolution, since sub-angstrom changes in position produce measurable current changes.

This distance dependence explains why tunneling becomes significant only at distances comparable to or smaller than the de Broglie wavelength of the tunneling particle. For electrons at moderate energies, the de Broglie wavelength is approximately 1 nanometer, matching the thickness of thin insulating layers where tunneling becomes important in semiconductor devices.

Controversies and open questions

The tunneling time debate

Despite its success in predicting tunneling probabilities and decay rates, quantum tunneling raises profound conceptual questions.

Chief among these is the question of tunneling time: how long does a particle remain inside the barrier while tunneling through?

Various interpretations have been proposed. Early treatments suggested that tunneling appears instantaneous—the particle emerges on the far side without spending time in the barrier.

Other approaches invoked different time concepts: phase time, group time, or dwell time. More recent experimental work, including studies using attosecond spectroscopy and measurements of Bose-Einstein condensate tunneling, has provided empirical constraints on tunneling time, though the question remains subtle and interpretation-dependent.

The 2025 experimental results challenging Bohmian mechanics through tunneling time measurements demonstrate that this debate remains active at the frontiers of quantum physics.

Macroscopic tunneling limits

Quantum tunneling generally occurs readily for microscopic particles like electrons but becomes vanishingly improbable for macroscopic objects. The exponential dependence of transmission probability on particle mass explains this: the transmission coefficient contains m in the exponent, so macroscopic tunneling is suppressed by factors of 10^10^23 or more.

Yet the 2025 Nobel Prize recognized the demonstration that macroscopic quantum systems—containing billions of particles acting collectively—can exhibit tunneling behavior. This revelation emerged from superconducting circuits where Cooper pairs tunnel collectively as a unified quantum object. Future research may reveal unexpected mechanisms for macroscopic tunneling in other collective quantum systems.

Tunneling beyond standard interpretations

Recent theoretical work explores tunneling mechanisms beyond conventional pictures. Some studies propose that tunneling in semiconductors involves virtual photons mediating electron-hole annihilation-recombination processes—an elegant hypothesis connecting tunneling to quantum electrodynamics.

Long-range tunneling studies suggest that under certain conditions, ultracold atoms can tunnel to distant traps mediated by matter-wave emissions, extending tunneling beyond the conventional wavelength-scale limitations.

These developments suggest that while tunneling’s fundamental mechanism is well understood through the Schrödinger equation’s wave-like solutions, the phenomenon’s full richness may yet contain surprises as experimental techniques probe previously inaccessible regimes.

What are the future directions?

Fundamental physics

Quantum tunneling illuminates the differences between quantum and classical mechanics, demonstrating that matter at small scales behaves according to principles of probability rather than determinism. This strangeness at the quantum level is not a limitation of our models but apparently a fundamental feature of nature.

Tunneling exemplifies how particles behave as waves, a central principle of quantum mechanics that bridges the deterministic classical world with the probabilistic quantum realm.

Practical innovation

Current applications of tunneling represent just the beginning. Future advances in quantum computing will harness tunneling effects in increasingly sophisticated ways. Emerging technologies explore Majorana fermions in topological materials—exotic quantum objects that may enable quantum error correction and fault-tolerant quantum computation. Energy storage devices continue advancing as researchers develop quantum tunneling-based batteries and supercapacitors with unprecedented energy density and charging speed.

Biological implications

Intriguingly, evidence suggests quantum tunneling may play roles in biological systems. Some enzymes appear to employ hydrogen tunneling in catalytic mechanisms, potentially enhancing reaction rates at room temperature.

Avian magnetoreception—the compass sense enabling bird migration—may involve quantum tunneling of electrons in specialized proteins. These biological applications remain areas of active investigation, though they hint that evolution may have learned to harness quantum mechanical effects in unexpected contexts.

Key takeaways

1. Quantum tunneling allows particles to cross barriers even when their energy is below the barrier height, defying classical physics predictions.
2. It occurs because particles behave as waves; their wave functions extend into and beyond barriers, giving a nonzero probability of appearing on the other side.
3. The probability of tunneling depends exponentially on the barrier’s width, height, and the particle’s mass—thinner, lower barriers and lighter particles increase tunneling.
4. Quantum tunneling underpins technologies such as scanning tunneling microscopes, flash memory, and quantum computers, as well as natural processes like radioactive decay and stellar fusion.
5. Experimentally confirmed countless times, tunneling reshaped understanding of matter, showing that at the quantum level, probability—not certainty—governs physical behavior.

 

---

References

1. Ashcroft, N.W. and Mermin, N.D. (1976) ‘Solid state physics’, Holt, Rinehart and Winston.
2. Binnig, G. and Rohrer, H. (1982) ‘Scanning tunneling microscopy’, IBM Journal of Research and Development, 44(3), 279–293.
3. Clarke, J., Devoret, M.H. and Martinis, J.M. (1984, 1985) ‘Resonant activation from the zero-voltage state of a current-biased Josephson Junction and energy-level quantization’, Physical Review Letters, 53, 1260; 55, 1543.
4. Condon, E.U. and Gurney, R.W. (1928) ‘Quantum mechanics and radioactive disintegration’, Nature, 122, 439.
5. Dingle, R.B. (1973) ‘Asymptotic expansions: their derivation and interpretation’, Academic Press.
6. Eigler, D.M. and Schweizer, E.K. (1990) ‘Positioning single atoms with a scanning tunnelling microscope’, Nature, 344, 524–526.
7. Esaki, L. and Miyahara, Y. (1960) ‘A new device using the tunneling process in narrow p-n junctions’, Solid-State Electronics, 1, 13–21.
8. Gamow, G. (1928) ‘Zur Quantentheorie des Atomkernes’, Zeitschrift für Physik, 51, 204–212.
9. Giaever, I. (1960) ‘Energy gap in superconductors measured by electron tunneling’, Physical Review Letters, 5, 147–148.
10. Hess, H.F., Robinson, R.B., Dynes, R.C., Valles, J.M. and Waltman, D.E. (1990) ‘Scanning-tunneling-microscope observation of a proximity-induced charge-density wave around a vortex in 2H-NbSe₂’, Physical Review Letters, 62, 214–216.
11. Hund, F. (1927) ‘Zur Deutung der Molekelspektren I’, Zeitschrift für Physik, 40, 742–764.
12. Jeffreys, H. (1923) ‘On certain approximate solutions of linear differential equations of the second order’, Proceedings of the London Mathematical Society, 23, 428–436.
13. Josephson, B.D. (1962) ‘Possible new effects in superconductive tunnelling’, Physics Letters, 1, 251–253.
14. Koch, J., Yu, T.M., Gambetta, J., Houck, A.A., Schuster, D.I., Majer, J., Blais, A., Devoret, M.H., Girvin, S.M. and Schoelkopf, R.J. (2007) ‘Charge-insensitive qubit design derived from the Cooper pair box’, Physical Review A, 76, 042319.
15. Mandelstam, L.I. and Leontovich, M.A. (1928) ‘Über Rayleighsche Strahlung’, Zeitschrift für Physik, 47, 131–143.
16. Martín-Palma, R.J. (2020) ‘Quantum tunneling in low-dimensional semiconductors mediated by virtual photons’, AIP Advances, 10(1), 015145.
17. Merzbacher, E. (2002) ‘The early history of quantum tunneling’, Physics Today, 55(8), 44–49.
18. Nordheim, L.W. (1927) ‘Zur Theorie der thermionischen Emission und der Elektronenemission aus Metallen’, Zeitschrift für Physik, 46, 833–855.
19. Schottky, W. (1931) ‘Zur Wellenmechanik des Tunneleffektes’, Physikalische Zeitschrift, 32, 913–915.
20. Schrödinger, E. (1926) ‘An undulatory theory of the mechanics of atoms and molecules’, Physical Review, 28, 1049–1070.
21. Shukla, K., Chen, P.S., Chen, J.R., Chang, Y.H. and Liu, Y.W. (2020) ‘Macroscopic matter wave quantum tunnelling’, Nature Communications Physics, 3, 211.
22. Tinkham, M. (2004) ‘Introduction to superconductivity’, 2nd edn. Dover Publications.
23. Yang, Y.X., Bai, S.Y. and An, J.H. (2025) ‘Long-range quantum tunneling via matter waves’, Nature Communications Physics, 16, 1.
24. Young, R., Ward, J. and Scire, F. (1972) ‘The topografiner: An instrument for measuring surface microtopography’, Review of Scientific Instruments, 43, 999–1011.